Topologia spațială

1. Introducere

În 1736, matematicianul Leonhard Euler a publicat lucrarea The Seven Bridges of Königsberg despre care se poate spune că stă la baza ramurii matematice cunoscute sub denumirea de topologie.
În anul 1970, pregătindu-se de recensământ, United States Census Bureau, a folosit toplogia matematică pentru a reduce erorile ce apăreau pe hărțile rezultate.
Astăzi în cadrul Sistemelor Geografice Informaționale (GIS) termenul poate fi definit ca “știința și matematica relațiilor utilizate pentru validarea geometriei entităților vectoriale și pentru o serie de operații cum ar fi analiza de rețea și de vecinătate” [Goodchild, M.F., și colab., 2005].
În sens mai larg, topologia descrie relațiile spațiale existente între obiecte folosind seturi de reguli pentru a observa cum entitățile vectoriale (puncte, linii, poligoane) împărtășesc geometria și spațiul.
Totodată topologia face diferența dintre modele GIS și cele non-topologice (Modelul Spaghetti).

2. Structura topologică

2.1 Elemente de bază și termeni specifici topologiei

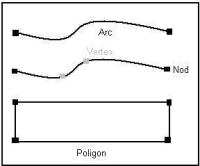
Sistemul vector se bazează pe primitive grafice. Primitiva grafică reprezintă cel mai mic element grafic utilizat la crearea și stocarea unei entități vectoriale. Sistemul vectorial folosește următoarele primitive grafice:

• Noduri – acestea definesc cele două extremități ale unui arc. Ele indică sensul de parcurgere al arcului.
• Vertecși – sunt reprezentați printr-o serie de puncte ce definesc forma unui arc (inflexiuni).
• Arce – sunt reprezentate de linia frântă dintre două noduri. Un arc trebuie să fie mărginit, obligatoriu, de un nod de pornire și unul de destinație.
• Poligoane – sunt definite ca suprafețe formate din arce închise. Unui poligon îi este atașat, mereu, un nod izolat numit centroid.

Figura 1. Primitive grafice

Așadar listele de noduri, arce, poligoane și vertecși, precum și relațiile de frontieră și cofrontieră puse în evidență prin adrese sau pointeri formează structura topologică de date [Nițu, C., și colab., 2002].

2.2 Relații topologice

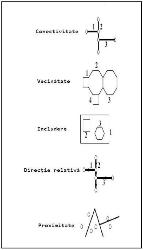
• Conectivitatea – indică ce obiecte spațiale sunt conectate cu altele, sau se intersecteză între ele (de exemplu un drum A se conectează cu un alt drum B).
• Vecinătatea – indică ce obiecte spațiale sunt vecine cu altele (două sau mai multe poligoane au în comun laturi sau granițe).
• Includerea – în acest caz obiectele spațiale (noduri, arce, poligoane mai mici) sunt conținute de un poligon.
• Proximitatea – indică ce obiecte spațiale sunt apropiate de altele.
• Direcția relativă – indică poziția relativă între obiectele spațiale.

Figura 2. Relații topologice

2.3 Concepte topologice

• Topologia de tip arc-nod
  Ține evidența arcelor conectate prin intermediul nodurilor comune. Aceasta definește lungimea, direcția și conectivitatea arcelor. Arcele sunt conectate dacă au în comun un nod.
• Topologia de tip poligon-arc
  Definește relațiile dintre arce și poligonul pe care îl definesc, precum și date privitoare la suprafață și vecinătate. Poligoanele sunt vecine dacă au în comun un arc. Pentru evitarea datelor redundante, poligoanele sunt stocate ca o listă de arce.
• Topologia de tip stânga-dreapta
  Această se referă la vecinătate și la modul cum poligoanele sunt asociate cu poligoanele vecine. În acest caz fiecare arc are o listă cu poligoanele existente în dreapta și stânga sa.

Figura 3. Modelul topologic al datelor [Nițu, C., și colab., 2002]

2.4 Reguli topologice generale

Topologia stochează o serie de parametri referitori la regulile aplicate, ranguri, toleranțe. De asemenea mai stochează și o serie de date legate de erori, excepții, etc.

• Regulile definesc relațiile admise între obiectele spațiale.
• Rangurile (ranks) controlează ce elemente ar putea fi mutate atunci când, regulile topologice existente în cadrul validării inițiale și pe parcursul validărilor ulterioare, se reunesc.
• Toleranța (Cluster tolerance) definește distanța minimă ce poate exista între două puncte, astfel încât acestea să fie considerate identice.
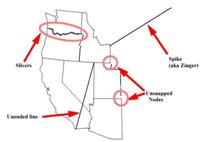
• Zonele cu erori (Dirty areas) reprezintă entitățile vectoriale ce au fost supuse unor editări ulterioare. Acestea permit limitarea zonei de verificat pentru erori în timpul validării topologice.
• Erorile și excepțiile sunt stocate în cadrul topologiei și permit gestionarea situațiilor în care elementele vectoriale nu se supun regulior specificate.

Figura 4. Erori topologice

3. Reguli topologice

3.1 Reguli aplicate entităților vectoriale de tip poligon

• Must Not Overlap (Nu trebuie sa se suprapună)
  Această regulă presupune ca interiorul poligoanelor din aceeași clasă de obiecte spațiale (feature class) să nu se suprapună. Poligoanele pot avea în comun noduri și margini, dar nu pot împărți aceeași suprafață. Un exemplu de folosire a acestei reguli este cazul entităților vectoriale ce reprezintă modul de utilizare a terenului, tipul formelor de relief, etc.

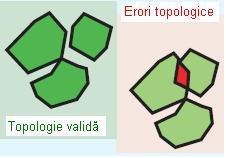
Figura 5. Must Not Overlap (ESRI – “Topology rules poster”, 2004)

• Must Not Have Gaps (Nu trebuie să conțină spații goale)
  Această regulă presupune ca între poligoane sau blocuri de poligoane învecinate să nu existe spații goale. Poligoanele pot avea în comun noduri, margini și suprafețe interioare. Este utilă atunci când este vorba de suprafețe continue, de exemplu tipurile de sol dintr-un anumit areal.

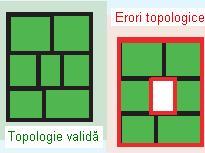
Figura 6. Must Not Have Gaps (ESRI – “Topology rules poster”, 2004)

• Must Not Overlap With (Nu trebuie să se suprapună peste)
  Această regulă presupune ca interiorul unui poligon ce aparține unei clase de obiecte spațiale nu trebuie să se suprapună peste interiorul unui poligon ce aparține altei clase de obiecte. Poligoanele pot avea în comun noduri și margini, sau pot fi complet separate. Se utilizează atunci când se intenționează îmbinarea a două sisteme ce se exclud reciproc, cum ar fi amenajarea teritoriului și arealele acoperite de apă.

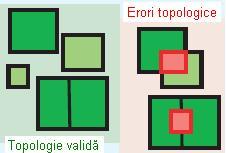
Figura 7. Must Not Overlap With (ESRI – “Topology rules poster”, 2004)

• Must Be Covered By Feature Class Of (Trebuie să fie acoperită de o clasă de obiecte spațiale)
  În acest caz se presupune că poligoanele dintr-o clasă de obiecte spațiale trebuie să fie acoperite de poligoanele dintr-o altă clasă de obiecte spațiale. Această regulă poate fi utilizată atunci cand un areal de un anumit tip, cum ar fi o țară, trebuie să fie acoperit în totalitate de areale de alt tip, cum ar fi județele.

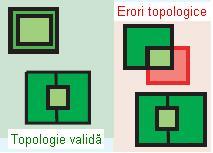
Figura 8. Must Be Covered By Feature Class Of (ESRI – “Topology rules poster”, 2004)

• Must Cover Each Other (Trebuie să se acopere unul pe altul)
  Regula în speță presupune ca un poligon aparținând unei clase de obiecte spațiale trebuie să aibă în comun întreaga suprafață cu un poligon aparținând altei clase de obiecte spațiale. Această regulă se folosește atunci când două poligoane aparținând a două clase de obiecte spațiale diferite acoperă aceeași suprafață. De exemplu clasa vegetație și clasa soluri trebuie să se acopere una pe celaltă.

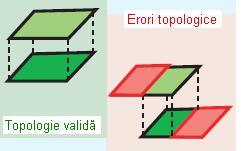
Figura 9. Must Cover Each Other (ESRI – “Topology rules poster”, 2004)

• Must Be Covered By (Trebuie să fie acoperit de)
  Această regulă presupune ca poligoanele ce aparține unei clase de obiecte spațiale să fie conținute total de poligoanele aparținând altei clase de obiecte spațiale. Este utilă atunci când se intenționează ca un set de poligoane să fie acoperite de un alt poligon ce aparține unei alte clase de obiecte spațiale. De exemplu clasa județe trebuie să fie acoperită de clasa țări.

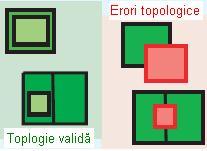
Figura 10. Must Be Covered By (ESRI – “Topology rules poster”, 2004)

• Boundary Must Be Covered By (Laturile trebuie să fie acoperite de)
  Această regulă prevede ca laturile unui poligon dintr-o clasă de obiecte spațiale trebuie să fie acoperite de liniile dintr-o altă clasă de obiecte. De regulă aceasta este utilă atunci când suprafața unei entități conține un set de atribute, iar limitele acesteia alt set de atribute. De exemplu clasa parcele poate fi stocată împreună cu limitele acestora intr-o bază de date spațială. Fiecare parcelă poate fi definită de una sau mai multe linii, fiecare dintre ele conținând diverse informații, iar parcelele respective trebuie să se potrivească perfect cu limitele sale.

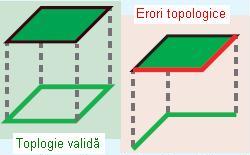
Figura 11. Boundary Must Be Covered By (ESRI – “Topology rules poster”, 2004)

• Area Boundary Must Be Covered By Boundary Of (Limitarea zonei tebuie să facă obiectul unei alte limite)
  Regula presupune ca laturile unui poligon dintr-o clasă de obiecte spațiale să fie acoperite de marginile altui poligon dintr-o altă clasă de obiecte spațiale. Este utilă cand un poligon aparținând unei clase de obiecte spațiale cum ar fi o subdiviziune, este compus din mai multe poligoane aparținând altei clase de obiecte spațiale cum ar fi clasa parcele, dar nu sunt acoperite în totalitate de ultima.

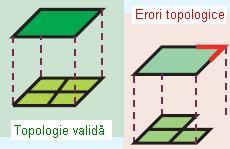
Figura 12. Area Boundary Must Be Covered By Boundary Of (ESRI – “Topology rules poster”, 2004)

• Contains point (Conține punct)
  În cazul acestei reguli, se presupune că un poligon aparținând unei clase de obiecte spațiale să conțină cel puțin un punct aparținând altei clase de obiecte spațiale. Punctul trebuie să fie în interiorul poligonului și nu pe marginea acestuia. Este utilă atunci cand poligonul trebuie sa aibă asociată cel puțin o entitate punctuală, ca de exemplu parcelele trebuie să aibă o adresă.

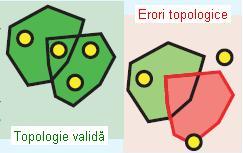
Figura 13. Contains point (ESRI – “Topology rules poster”, 2004)

3.2 Reguli aplicate entităților vectoriale de tip linie

• Must Not Overlap (Nu trebuie sa se suprapună)
  Această regulă presupune ca liniile din cadrul aceleași clase de obiecte spațiale să nu se suprapună. Este folosită atunci cand liniile nu trebuie sa fie dublate, de exemplu o rețea hidrografică. Liniile se pot intersecta, dar nu pot avea segmente comune.

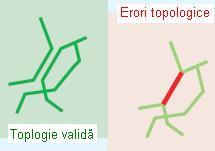
Figura 14. Must Not Overlap (ESRI – “Topology rules poster”, 2004)

• Must Not Intersect (Nu trebuie să se intersecteze)
  Regula de față presupune ca liniile aparținând aceleași clase de obiecte spațiale să nu se intersecteze sau să se suprapună, însă pot avea în comun puncte de capăt.

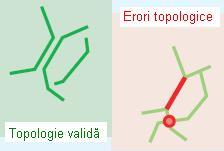
Figura 15. Must Not Intersect (ESRI – “Topology rules poster”, 2004)

• Must Not Have Dangles (Nu trebuie să aibă discontinuități)
  Regula în speță prevede ca liniile existente în cadrul aceleiași clase de obiecte spațiale trebuie să fie conectate la capete. Această regulă este folosită atunci când liniile formează o suprafață, de exemplu când definesc un poligon, sau când sunt conectate asemănator unei rețele stradale. În ultimul caz, regula poate fi încălcată atunci când străzile se închid brusc.

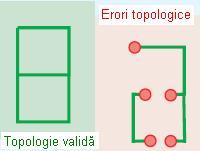
Figura 16. Must Not Have Dangles (ESRI – “Topology rules poster”, 2004)

• Must Not Have Pseudo-nodes (Nu trebuie să conțină pseudo-noduri)
  Această regulă presupune ca o linie să fie conectată cu cel puțin alte două la fiecare capăt. O linie ce este conectată cu doar o singură altă line, sau cu ea însăși, se presupune că are pseudo-noduri. Această regulă este utilizată în cazul în care o linie trebuie să formeze bucle închise, cum ar fi atunci când acestea definesc limite de poligoane.

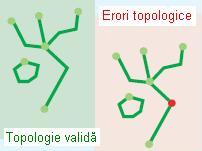
Figura 17. Must Not Have Pseudo-nodes (ESRI – “Topology rules poster”, 2004)

• Must Not Intersect Or Touch Interior (Nu trebuie să se intersecteze sau să se atingă în interior)
  Regula presupune ca o linie aparținând aceleiași clase de obiecte spațiale să atingă o altă linie doar la capete. Orice segment ce se suprapune sau se intersectază în alt loc decăt la capete, reprezintă o eroare. Regula este utilă atunci când este vorba de linii ce reprezintă parcele.

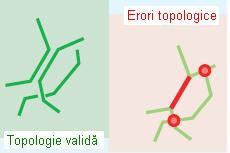
Figura 18. Must Not Intersect Or Touch Interior (ESRI – “Topology rules poster”, 2004)

• Must Not Overlap With (Nu trebuie să se suprapună peste)
  Această regulă presupune ca o linie ce aparține unei clase de obiecte spațiale să nu se suprapună peste o linie ce aparține altei clase de obiecte. Regula este folosită atunci când liniile nu trebuie să ocupe același spațiu, de exemplu drumurile nu trebuie să se suprapună cu liniile de cale ferată.

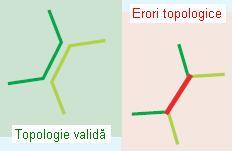
Figura 19. Must Not Overlap With (ESRI – “Topology rules poster”, 2004)

• Must Be Covered By Feature Class Of (Trebuie să fie acoperită de o clasă de obiecte spațiale)
  Această regulă presupune ca liniile ce aparțin unei clase de obiecte spațiale să fie acoperite de liniile ce aparțin altei clase de obiecte. Este folosită când un grup de linii descrie aceeași enitate spațială. De exemplu ruta unui autobuz trebuie să acopere rețeaua stradală.

Figura 20. Must Be Covered By Feature Class Of (ESRI – “Topology rules poster”, 2004)

• Must Be Covered By Boundary Of (Trebuie să fie acoperite de laturi)
  În cazul acesta o liniile ce aparține unei anumite clase de obiecte spațiale trebuie să fie acoperite de laturile unui poligon ce aparțin altei clase de obiecte spațiale. De exemplu liniile ce formează o parcelă trebuie să corespundă cu marginile poligonului parcelei respective.

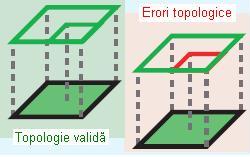
Figura 21. Must Be Covered By Boundary Of (ESRI – “Topology rules poster”, 2004)

• Endpoint Must Be Covered By (Capătul trebuie să fie acoperit de)
  Regula presupune ca limitele liniilor dintr-o clasă de obiecte spațiale să fie acoperite de puncte dintr-o altă clasă de obiecte spațiale. Este utilă atunci când se intenționează ca intersecția unei străzi să se afle la joncțiunea a două străzi.

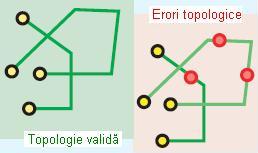
Figura 22. Endpoint Must Be Covered By (ESRI – “Topology rules poster”, 2004)

• Must Not Self Overlap (Nu trebuie să se suprapună cu ea însăși)
  Regula prevede ca liniile să nu se suprapună cu ele însele. Ele se pot intersecta dar nu trebuie să aibă segmente comune. Această regulă este utilă în special în analiza transporturilor, de exemplu o stradă nu trebuie să se suprapună peste o autostradă.

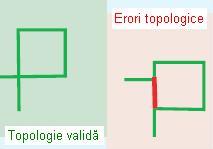
Figura 23. Must Not Self Overlap (ESRI – “Topology rules poster”, 2004)

• Must Not Self Intersect (Nu trebuie să se intersecteze cu ea însăși)
  În acest caz liniile nu trebuie să se intersecteze sau să se suprapună cu ele însele. Este utilă în cazul curbelor de nivel.

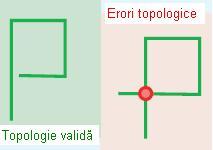
Figura 24. Must Not Self Intersect (ESRI – “Topology rules poster”, 2004)

• Must Be Single Part (Trebuie să fie un singur segment)
  Această regulă presupune ca linia să fie compusă dintr-un singur segment. Poate fi folosită atunci când linia nu trebuie să fie compusă din mai multe segmente, cum ar fi de exemplu o linie ce reprezintă o autostradă.

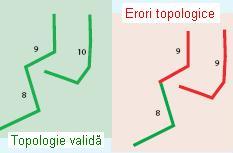
Figura 25. Must Be Single Part (ESRI – “Topology rules poster”, 2004)

3.2 Reguli aplicate entităților vectoriale de tip punct

• Must Be Covered By Boundary Of (Trebuie să fie acoperite de laturi)
  Regula presupune ca punctele ce aparțin unei clase de obiecte spațiale să intersecteze laturile unui poligon aparținând unei alte clase de obiecte spațiale. Se utilizează spre exemplu pentru markerii de frontieră în cazul parcelelor.

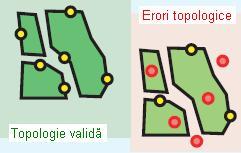
Figura 26. Must Be Covered By Boundary Of (ESRI – “Topology rules poster”, 2004)

• Must Be Properly Inside Polygons (Trebuie să fie în interiorul poligoanelor)
  În acest caz punctele trebuie să se găsească în interiorul unui poligon. Regula este utilă atunci când caracteristicile punctelor relaționează cu poligoanele. De exemplu reședințele de județ reprezentate punctual trebuie să se găsească în interiorul județelor reprezentate prin poligoane.

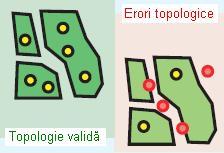
Figura 27. Must Be Properly Inside Polygons (ESRI – “Topology rules poster”, 2004)

• Must Be Covered By Endpoint Of (Trebuie să fie acoperite de capete)
  Regula prevede ca punctele ce se găsesc într-o clasă de obiecte spațiale să fie acoperite de capetele liniilor ce se găsesc într-o altă clasă de obiecte spațiale. Regula este similară cu regula aplicată liniilor „Endpoint Must Be Covered By”. Un exemplu de aplicabilitate pentru această regulă este cazul intersecțiilor de străzi.

Figura 28. Must Be Covered By Endpoint Of (ESRI – “Topology rules poster”, 2004)

• Must Be Covered By Line (Trebuie să fie acoperite de o linie)
  Regula prevede ca punctele ce se găsesc într-o clasă de obiecte spațiale să fie acoperite linii ce se găsesc într-o altă clasă de obiecte spațiale. Poate fi utilizată pentru stațiile de măsurare a debitelor ce trebuie să se situeze pe cursurile râurilor.

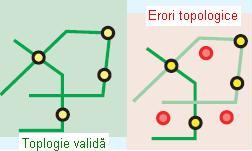
Figura 29. Must Be Covered By Line (ESRI – “Topology rules poster”, 2004)

Bibliografie

1. ESRI – “Building a Geodatabase”.
2. ESRI – “Topology rules poster”, 2004.
3. “Fundamental Geospatial Concepts – spatial relationship and topology”
4. Imbroane, A.M., Moore, D., – “Inițiere in GIS și Teledetecție”, Presa Universitară Clujeană, 1999.
5. Longley, P.A., Goodchild, M.F., Maguire, D.J., Rhind, D.W. – „Geographic Information System and Science”, Second Edition, 2005.
6. Nițu, C., Nițu, C.D., Tudose, C.E., Vișan, M.C., – “Sisteme Informaționale Geografice și Cartografie computerizată”, Editura Universității din București, 2002.
7. Theobald, D.M., – “Understanding Topology and Shapefiles”, 2001