Prelucrarea datelor geospațiale folosind limbajul R

Introducere

Limbajul R (http://www.r-project.org) este un mediu relativ nou de analiză statistică și vizualizare a seturilor de date. În prezent parte a proiectului GNU, R a fost dezvoltat în anii ’90 în Auckland, Noua Zeelandă, de către Ross Ihaka și Robert Gentleman. Fiind o implementare a limbajului S în mediul open-source, inițial limbajul R dispunea numai de tehnici de analiză statistică clasică. Spre sfârșitul anilor ‘90 apar primele funcții de analiză statistică a seturilor de date spațiale (Venables și Ripley, 1999), acestea costituind primul pas în implementarea claselor de date spațiale în R.

Popularitatea limbajului R a fost determinată atât de capacitatea de a rula pe orice tip de platformă (Linux, MacOS X, Windows), cât și de existența a unui număr impresionant de programe suplimentare (biblioteci) care completează sistemul de bază (în momentul de față sunt 96 de biblioteci disponibile în categoria ‘Spatial’ – http://cran.r-project.org/web/views/Spatial.html).

O altă caracteristică importantă a acestui limbaj este posibilitatea de a accesa orice funcție disponibilă sub formă de linie de comandă în sistemul de operare sau funcțiile altor softuri GIS direct sau prin intermediul unor biblioteci suplimentare. Astfel utilizând limbajul R putem apela funcțiile suitelor GDAL, SAGA-GIS (RSAGA), GRASS (spgrass6), ILWIS și chiar funcțiile din Geoprocessing Tool din ArcGIS (RPyGeo).

Limbajul R face parte din categoria limbajelor de programare orientate pe obiect , proprietate care se traduce prin faptul că o funcție poate avea acțiuni diferite, determinate de tipul de clasă al obiectului căruia i se adresează.

Cu toate că există câteva aplicații care ne oferă posibilitatea accesări anumitor funcții R printr-o interfață GUI (RCmdr și Rattle), cel mai des limbajul R este utilizat direct în linia de comanda, rezultând astfel capacitatea de automatizare a întregului proces de prelucrare a datelor. Această proprietate poate constituite și un dezavantaj dacă ne gândim că de ficecare dată când facem ceva nou este necesar să învățăm alte comenzi. Alt minus al limbjului R este dat și de timpul de procesare al seturilor mari de date care este condiționat de capacitatea memoriei RAM sistemului de calcul.

Prin utilizarea mediilor de dezvoltare integrate (IDE) putem eficientiza scrierea scripturilor în limbajul R. Cele mai cunoscute astfel de aplicații sunt Tinn-R (http://sciviews.org/Tinn-R/) și RStudio (http://rstudio.org/). Cu ajutorul lor putem vizualiza mai bine sintaxa acestui limbaj cât și proprietățile obiectelor încărcate în spațiul de lucru. De notat că RStudio este independent de sistemul de operare în timp ce Tinn-R se poate utiliza doar sub Windows.

Puterea exemplului

Cele 96 de biblioteci dedicate claselor din categoria ‘Spatial’, multitudinea de tehnici de analiză statistică disponibile și posibilitatea accesării funcțiilor altor aplicații
GIS fac din limbajul R o unealtă foarte puternică de analiză și procesare a datelor spațiale.

Cel mai eficient mod de a susține acest lucru se poate realiza prin explicarea și rularea linie cu linie a unui script în care sunt prezentate câteva metode de interpolare aplicate în spațializarea unui parametru climatic – temperatura medie lunară ianuarie 2005. Deoarece principală țintă a acestui articol este de a fi prezentate capabilitățile limbajului R în manipularea datelor spațiale, se vor folosi strict bibliotecile dispoinibile în R. Librăriile utilizate în acest articol pot fi instalate prin rularea în consola limbajului R a comenzii:

source('http://www.geo-spatial.org/vechi/file_download/27418/il_intro_sr.R')

Pentru interpolarea valorilor medii lunare de temperatură s-au folosit 6 metode de interpolare care se pot grupa în două categorii: metode uni-variate (folosesc în interpolare doar datele înregistrate la stațiile meteorologice) și metode multi-variate (beneficiază de aportul variabilelor explicative în interpolare – predictori derivați din MNT). Cele 6 metode sunt: IDW (Inverse Distance Weighting), TPS (Thin Plate Spline), OK (Ordinary Kriging), MLR (Multiple Linear Regression), GWR (Geographically Weighted Regression GWR) și UK (Universal Kriging).

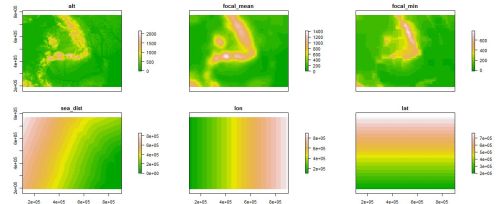
În această prezentare s-au utilizat 6 predictori derivați din MNT: altitudinea, câmpul de latitudine, câmpul de longitudine, altitudinea medie pe o rază de 50 km, altitudinea minimă pe o rază de 50 km și distanța față de Marea Neagra, la o rezoluție spațială de 3km². Pentru generarea acestor predictori la rezoluția specificată s-a folosit MNT-ul disponibil în secțiunea de Download a geo-spatial, a cărui rezoluție spațială este de 80 m². Prin utilizarea bibliotecii raster MNT-ul este transformat la 3km² rezoluție spațială:

download.file('http://www.geo-spatial.org/vechi/file_download/1247','dem.zip',mode="wb")
unzip('dem.zip')
library(raster)
dem<-raster('mozaic_ro.tif')
projection(dem)<-" +init=epsg:3844"
dem.a <- aggregate(dem, fact=37.5, fun=mean,progress='text')
plot(dem.a,col=terrain.colors(21))
show(dem.a)

Partea de descărcare și dezarhivare se poate realiza direct în R, procesarea MNT-ului realizându-se prin funcția aggregate() a bibliotecii raster printr-un factor de 37,5 rezultând astfel un MNT cu rezoluția spațială de 3040 m², după cum putem vede utilizând comanda show(). O imagine a MNT-ului ne este oferită de comanda plot() prin utilizarea unei palete de culori adecvate, după cum reiese și din nume.

Cu MNT-ul adus la scara spațială dorită se poate începe extragerea celorlalți predictori. Altitudinea medie și minimă pe o rază de 50 km se poate obține prin utilizarea funcției focal() , disponibilă în aceeași bibliotecă, luându-se în calcul 17 vecini, ceea ce reprezintă corespondentul aproximativ al unei raze de 50 km:

focal_mean<-focal(dem.a, ngb=17, fun=mean,progress='text')
plot(focal_mean)
show(focal_mean)
focal_min<-focal(dem.a, ngb=17, fun=min,progress='text')
plot(focal_min)
show(focal_min)

Pentru calcularea distanței față de Marea Neagră s-a folosit o mască în format vector cu această unitate geografică. Deoarece intenția acestui articol este de a se utilizeze datele disponibile online, această mască a fost extrasă din biblioteca mapdata, care pune la dispoziție un set de date globale cu granițele țărilor, nu foarte actualizate. Librăria maptools ne ajută să convertim granițele extrase din formatul map în formatul SpatialPolygonsDataFrame. Un aspect dificil în R îl constituie faptul că de cele mai multe ori fiecare bibliotecă lucrează cu clase proprii de date. Din fericire întodeauna există funcții care convertesc datele dintr-o clasă în altă. Pentru aflarea tipului de clasă al unor seturi de date încărcate în R se utilizează comanda class():

library(mapdata)
m<-map("worldHires", xlim = c(20,31), ylim = c(42,48), plot=F, fill=TRUE, col="transparent") 
id <- sapply(strsplit(m$names, ":"), function(x) x[1])
class(m)
library(maptools)
m2 = map2SpatialPolygons(m,IDs=id,proj4string=CRS("+proj=longlat"))
class(m2)
m2.st <- spTransform(m2, CRS("+init=epsg:3844"))
summary(m2.st)
plot(m2.st)

Masca în format SpatialPolygonsDataFrame este reproiectată din WGS84 în Stereo70 prin funcția spTransform din biblioteca rgdal, bibliotecă care este încarcată automat în momentul când se rulează funcția raster din biblioteca raster. Cu masca astfel obținută se poate trece la calculul distanței fiecărui pixel de pe teritoriul României față de Marea Neagră:

r2 <- rasterize(m2.st, dem.a,mask=TRUE,progress='text')
plot(r2,col=heat.colors(21))
library('igraph')
sea_dist<- gridDistance(r2,origin=NA, progress='text')
plot(sea_dist,col=heat.colors(21))

Prin funcția rasterize() se alocă pixelilor corespunzători Mării Negre NA, iar prin gridDistance() se calculează distanța de la pixelii NA la fiecare pixel cu valori disponibile. Cele două funcții sunt parte componentă a raster, cu mențiunea că gridDistance() folosește anumite funcții din biblioteca igraph.

Cei 4 predictori calculați pot fi grupați într-un obiect de tip brick raster care este corespondentul unui fișier grid cu mai multe benzi :

par.col<-brick(dem.a,focal_mean,focal_min,sea_dist)
layerNames(par.col)<-c("alt", "focal_mean", "focal_min","sea_dist")
plot(par.col)
class(par.col)

Pentru derivarea câmpurilor de longitudine și latitudine din MNT cei patru predictori sunt convertiți din clasa de tip brick în clasa de tip SpatialGridDataFrame specifică bibliotecii sp, un alt pachet care lucrează cu date spațiale:

par.sp<-as(par.col,'SpatialGridDataFrame')
class(par.sp)
#adauga campurile de longitudine si latitudine
par.sp@data[,'lon']<-coordinates(par.sp)[,1]
par.sp@data[,'lat']<-coordinates(par.sp)[,2]
summary(par.sp)
class(par.sp)
plot(brick(par.sp),col=terrain.colors(21))

Figura 1. Predictori derivați din MNT – rezoluție spațială 3040 m².

Ultimile două variabile extrase rezultă practic din coordonatele fiecărui pixel care compun obiectul par.sp. Prin funcția summary() avem acces la proprietățile obiectului de tip sp, putându-se astfel vizualiza sumarul statistic al fiecărui strat. Vizualizarea tuturor stratelor se poate face sincron prin utilizarea funcției plot().

Fișierul cu stații meteo este obținut din aceeași secțiune a geo-spatial, iar tabelul cu datele de temperatură este citit direct de pe același server. Prin utilizarea unui câmp comun se unesc cele două tabele utilizând funcția merge():

#descarca statii meteo
download.file('http://www.geo-spatial.org/vechi/file_download/25523/statii_meteo_4326.zip','meteo.zip',mode = "wb")
unzip('meteo.zip')
meteo<-readOGR(getwd(),"statii_meteo_4326")
meteo<-meteo[meteo$NUME!='GLORIA'  , ]
summary(meteo)
#transforma in Stereo 70
meteo_st <- spTransform(meteo, CRS("+init=epsg:3844"))
print(summary(meteo_st))
tt<-read.csv('http://www.geo-spatial.org/vechi/file_download/27415/tt_01_2005.csv', na.string="-")
tt<-na.omit(tt)
summary(tt)
hist(tt$temp_medl)
tt.co<-merge(meteo_st, tt, by.x="CODGE", by.y="cod")
coordinates(tt.co)<-~coords.x1+coords.x2
proj4string(tt.co)<-proj4string(meteo_st)
spplot(tt.co['temp_medl'])

Pin funcția hist() ne putem face o idee asupra distribuției de frecvență a datelor, iar spplot() ne oferă posibilitatea vizualizării distribuției spațiale a datelor de temperatură din obiectul de tip SpatialPointsDataFrame, care este corespondentul unui fișier *.shp de tip puncte.

Pentru testarea relației dintre variabila dependentă și variabilelor independente s-au extras la punctul fiecărei stații valorile fiecărui predictor utilizându-se funcția over():

#extrage valorile la statie din par.sp
ov<-over(tt.co,par.sp)
tt.co$alt<-ov$alt
tt.co$focal_mean<-ov$focal_mean
tt.co$focal_min<-ov$focal_min
tt.co$sea_dist<-ov$sea_dist
tt.co$lon<-ov$lon
tt.co$lat<-ov$lat
summary(tt.co)

Astfel s-a adăugat câte o coloană cu valorile extrase din par.sp pentru fiecare punct al obiectului tt.co. Analiza relației dintre temperatura medie lunară și variabilele explicative s-a realizat prin regresia multiplă liniară, utilizându-se funcția lm().

#construieste ecuatia de regresie
regres<-lm(temp_medl~alt+focal_min+focal_mean+sea_dist+lon+lat,tt.co)
summary(regres)

Prin funcția summary() s-au vizualizat rezultatele regresiei care ne relevă un coeficient R² de 0.924, putându-se astfel afirma că cele 6 co-variabile explică peste 90% din variabilitatea spațială a temperaturii. De asemenea intensitatea puternică a relației statistice dintre cele două seturi de date este confirmată și de semnificația statistică a coeficientului de determinare, cu o probabilitate de eroare foarte mică.

Pentru interpolarea pri metoda TPS s-a utilizat funcția Tps() din biblioteca fields. Parametrul de netezire este ales de această funcție în mod automat printr-un proces iterativ de validare încrucișată generalizată:

#ThinPlateSpline
library(fields)
tps<-Tps(coordinates(tt.co), tt.co$temp_medl)
tps.v<-predict(tps,coordinates(par.sp))
par.sp@data[,'TPS']<-tps.v
spplot(par.sp['TPS'],col.regions=rev(heat.colors(16)))

Cu ajutorul funcției predict() se estimează valorile de temperatură în toate punctele de grilă ale par.sp, spre deosebire de Tps() care estimează doar pe o suprafață a cărei extindere este limitată de datele cu mărimi cunoscute (tt.co). Funcția predict() returnează valorile sub forma unei matrice cu 1 coloană, a cărei ordine corespunde cu cea de scrierea a valorilor în SpatialGridDataFrame.

Pentru interpolarea utilizând IDW și OK s-au folosit funcțiile idw() și krige() disponibile în biblioteca gstat, unul din pachetele dedicate exclusiv analizei geo-statistice:

library(gstat)
#IDW
idw<-idw(temp_medl~1,tt.co,par.sp,idp=3)
names(idw)[1]<-'IDW'
spplot(idw['IDW'],col.regions=rev(heat.colors(16)))
#OrdinaryKriging
#construim variograma
v<-variogram(temp_medl~1,tt.co, width=20000)
plot(v)
v.f<-vgm(psill=8, model="Exp", nugget=2, range=100000)
plot(v,v.f)
v.f
#constrim suprafata
ok<-krige(temp_medl~1,tt.co,par.sp,v.f,debug.level=-1)
names(ok)[1]<-'OK'
spplot(ok['OK'],col.regions=rev(heat.colors(16)))

Funcțiile variogram() și vgm() construiesc variograma experimentală respectiv teoretică, parametrii celei din urmă fiind utilizați în metoda OK.

Pentru construirea suprafeței prin MLR s-a utilizat funcția krige(), în care se specifică parmaterii de intrare ai ecuației (variabilă dependentă – variabile independente), obiectul care conține datele de intrare tt.co și predictorii par.sp care ne ajută să estimăm în spațiu valorile de temperatură prin această metodă :

#RegresieMultiplaLiniara
mlr<-krige(formula(regres),tt.co,par.sp)
names(mlr)[1]<-'MLR'
spplot(mlr['MLR'],col.regions=rev(heat.colors(16)))

Metoda GWR este implementată în biblioteca spgwr. Acest tip de regresie presupune construirea unei ecuații de regresie pentru fiecare punct pentru care se realizează estimarea, distanța de selecție a punctelor fiind aleasă prin utilizarea procedurii de validare încrucișată gwr.sel():

#RegresiaGeograficPonderata
library(spgwr)
b.gwr <- gwr.sel(formula(regres), data=tt.co)
gwr <- gwr(formula(regres), tt.co,bandwidth=b.gwr)
gwr.f <- gwr(formula(regres), tt.co,bandwidth=b.gwr,fit.points = par.sp, predict=TRUE)
str(gwr.f)
names(gwr.f$SDF)[9]<-"GWR"
spplot(gwr.f$SDF['GWR'],col.regions=rev(heat.colors(16)))
par.sp$GWR<-gwr.f$SDF@data$GWR

Metoda Universal Kriging (Residual Kriging, Regression Kriging) este o metodă hibridă care presupune construirea unei suprafețe prin utilizarea regresiei multiple și corectarea acesteia prin însumarea cu suprafața reziduurilor de estimare ale regresiei, suprafață obținută prin interpolarea OK. Din fericire funcția krige() face toți acești pași, bineînțeles după ce parametrii variogramei sunt cunoscuți:

#UniversalKriging
v<-variogram(formula(regres),tt.co)
plot(v)
v.f<-vgm(psill=0.5, model="Sph", nugget=0.2, range=75000)
plot(v,v.f)
v.f
uk<-krige(formula(regres),tt.co,par.sp,v.f, debug.level=-1)
names(uk)<-'UK'
spplot(uk['UK'],col.regions=rev(heat.colors(16)))

Pentru vizualizarea într-o singură fereastră cele 6 suprafețe ale temperaturii medii lunare sunt grupate într-un obiect de clasă SpatialGridDataFrames și transformate într-o clasă de tip brick:

tt.map<-cbind(idw["IDW"],par.sp["TPS"],ok["OK"],mlr["MLR"],par.sp["GWR"],uk["UK"])
rtt.map<-brick(tt.map)
rtt.map@data@values[rtt.map@data@values>max(tt.co$temp_medl)]<-max(tt.co$temp_medl)
rtt.map@data@values[rtt.map@data@values < min(tt.co$temp_medl)]<-min(tt.co$temp_medl)
grtt.map <- projectRaster(rtt.map, crs=proj4string(meteo), progress='text')

Valorile din obiectul rtt.map care depășesc minimul și maximul temperaturilor măsurate au fost ajustate înainte de a fi reproiectat în proiecție geografică WGS84.

Înainte de vizualizare cele 6 straturi au fost decupate folosindu-se fișierul cu frontiere disponibil pe geo-spatial. Pentru această operație s-a aplicat aceeași funcție rasterize() din biblioteca raster.

#pt clip tara descarca frontiere
download.file('http://www.geo-spatial.org/vechi/file_download/1251','fro.zip',mode = "wb")
unzip('fro.zip')
front<-readOGR(getwd(),"frontiera_ro")
plot(front)
summary(front)
proj4string(front)<-projection(grtt.map)
br<-brick(nrows=208,ncols=287,extent(grtt.map),crs=proj4string(front),nl=6)
for( i in 1: nlayers(grtt.map))
{
print(i)
grtt.map<-addLayer(grtt.map, rasterize(front,grtt.map[[i]], mask=T, progress='text'))
}
grtt.map<-dropLayer( grtt.map, 1:6)
layerNames(grtt.map)<-layerNames(rtt.map)

Paleta de culori a fost generată cu ajutorul funcției brewer.pal() din biblioteca RColorBrewer. Prin utilizarea funcției spplot() sunt vizualizate cele 6 hărți din grtt.map, având o singură legendă și aceleași intervale de valori:

#harta finala
library(RColorBrewer)
brk<-seq(round(min(tt.co$temp_medl)),round(max(tt.co$temp_medl)), by=1)
cols <- append(rev(brewer.pal(9,"Blues")),brewer.pal(6,"Reds"))
gran<-list('sp.polygons',front, col='black',first=FALSE)
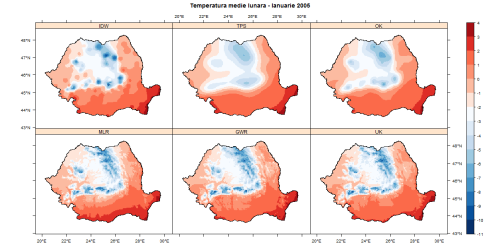
spplot(grtt.map,col.regions=cols,colorkey=list(space='right', at = brk, labels=list(at=brk),title="Celsius"),at=brk,layout=c(3,2),
main="Temperatura medie lunara - Ianuarie 2005",sp.layout=list(gran),scales=list(draw=T))

Figura 2. Temperatura medie lunară ianuarie 2005 – rezoluție spațială 3040 m².

Se observă clar o diferență între cele 2 categorii de metode, influența variabilelor explicative fiind determinantă pentru metodele multi-variate, dependența temperaturii medii fața de topografie fiind foarte bine reprezentată.

Concluzii

Fără a avea pretenția unei analize cantitative a metodelor de interpolare, cele prezentate mai sus încearcă să atragă atenția asupra unui alt instrument de procesare a datelor spațiale, care dispune de un număr impresionant de tehnici de analiză statistică. Chiar dacă uneori lucrul cu aplicațiile în linie de comandă este dificil nu trebuie neglijată posibilitatea automatizării anumitor proceduri de analiză a datelor care sunt livrate în flux operativ.

Comenzile prezentate mai sus pot fi rulate linie cu linie prin încărcare scriptului Spatia_Intro_R în mediul R.