Harta temperaturii medii lunare: metoda detrended kriging
de Alexandru Dumitrescu
Spațializarea (interpolarea) datelor se poate realiza printr-o serie de metode ce descriu dependența datelor învecinate, dintr-un set de date, într-un sistem Cartezian de coordonate. Mai exact prin interpolare se poate afla valoarea unui punct dat în funcție de măsurătorile efectuate în imediata apropiere acelui punct, utilizând o serie de funcții matematice. În climatologie, pentru obținerea unei suprafețe continue, metodele de interpolare folosite combină datele meteorologice cu alte elemente geografice.
În următoarele rânduri voi prezenta o metoda de realizarea a hărții medii lunare a temperaturii aerului folosind metoda detrend kriging (cazul simplu) utilizând SAGA GIS.
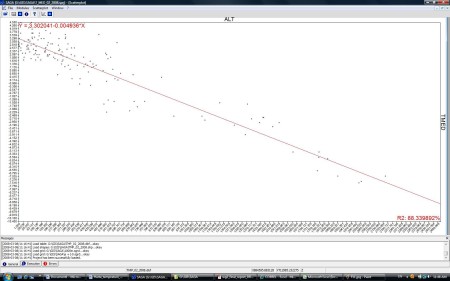
După cum se știe principalul factor climatologic care influențează distribuția spațială a temperaturii aerului este suprafața subiacentă prin formele ei de relief. De aceea, in conceperea hărții de temperatură, trebuie întotdeauna să luăm în calcul contribuția semnificativă pe care o are relieful în determinarea regimului termic al unei regiuni geografice. Dependența dintre temperatura medie lunară a aerului și altitudine se poate observa în figura 1, unde remarcăm că altitudinea explică 88 % din variabilitatea spațială a temperaturii.
Figura 1. Graficul corelației temperatură-altitudine.
Pentru a argumenta cele prezentate mai sus voi realiza harta repartiției temperaturii medii lunare a aerului, pe teritoriul României, utilizând modelul numeric al terenului având rezoluția de 1 km2.
Principalii pași parcurși în realizarea hărții sunt:
- folosirea gradientului vertical 0.65°C/100m ca tendință pentru stabilirea câmpului TM0nm (temperatura la nivelul mării)
TM = temperatura aerului înregistrată la nivelul stației meteorologice
a = – 0.0065°C/m
Z = altitudinea stației meteorologice (metri)
- interpolarea câmpului TM0nm folosind metoda ordinary kriging
- adăugarea tendinței câmpului interpolat TM0, folosind modelul numeric al terenului, obținându-se astfel harta finala TMED
Pentru realizarea hărții voi utiliza softul SAGA (System for Automated Geoscientific Analyses), aplicație GIS open source, modelul numeric SRTM 30 (1 km2) și date de temperatură înregistrate la stațiile meteorologice din România, în luna februarie 2008 (în format puncte .*shp). Modelul numeric al terenului poate fi importat folosind arhicunoscuta suită GDAL, implementată în SAGA, urmând calea Import/Export-Grids via GDAL. Formatul ESRI Shapfile este recunoscut implicit de această aplicație GIS.
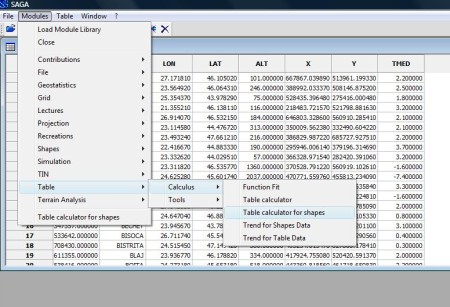
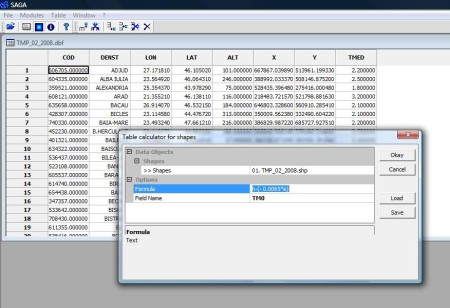
Având datele de temperatură in SAGA putem face calculul tabelar, pentru a reduce valorile de temperatură la nivelul de 0 metri, in tabelul cu atribute al fișierului .shp. Pentru aceasta vom folosi funcția Table calculator for shapes din Modules-Table-Calculus (figura 1). Aici vom selecta în câmpul Shape fișierul interesat (TMP_02_2008.shp în cazul de față) iar în câmpul Formula introducem h-(- 0.0065*e) folosind Field name-ul *TM0 (figura 2).
Figura 2. Calea către funcția Table calculator for shapes.
Figura 3. Aplicarea formulei de calcul tabelar in SAGA.
De reținut faptul că în SAGA coloanele tabelului cu atribute sunt indexate cu litere, astfel in formulă vom folosi litera h pentru coloana cu datele de temperatura și litera e pentru coloana care conține valorile de altitudine ale stațiilor meteorologice. De asemenea coloana TM0 va fi creată automat nefiind necesară existența ei înainte da a se aplica formula.
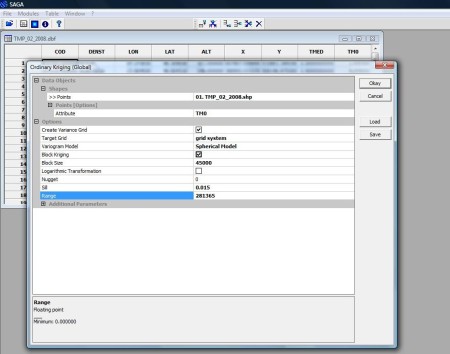
Următorul pas este interpolarea valorilor de temperatură , aduse la nivelul 0 metri, folosind metoda Orinary Kriging (Global) din Modules-Geostatistics-Kriging (figura 3).
Figura 4. Parametrii interpolării.
Nu voi insista asupra importanței fiecărui parametru al interpolării (probabil aceștia vor face obiectul altei prezentări), ce trebuie avut în vedere este faptul că valorile coeficienților interpolării depind de distribuția statistica a șirului de date care vor fi interpolate. Pentru harta temperaturii medii pot fi folosiți acești coeficienți, cu mici ajustări, în funcție de „harta erorilor” (Ordinary Kriging Variance).
După rularea modului Ordinary Kriging (Global) obținem harta temperaturii la nivelul 0 (TM0) (figura5) cat și harta varianței suprafeței interpolate („harta erorilor”) (figura 6).
Figura 5. Harta temperaturii TM0.
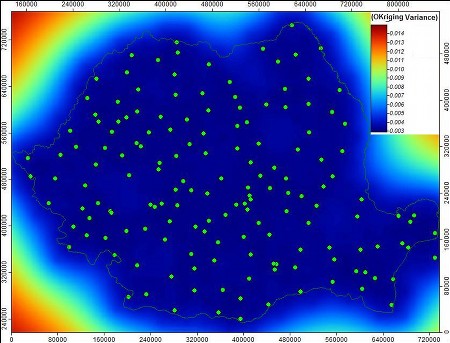
Figura 6. Harta erorilor suprafeței interpolate TM0.
Din analiza figurii 6 se poate observa o strânsă legătură între densitatea punctelor, reprezentând stațiile meteorologice, și erorile prezente în interpolare: astfel cu cât numărul punctelor este mai redus într-o anumită regiune cu atât erorile sunt mai mari, ajungându-se la un maxim în zonele din apropiere a graniței unde suprafața rezultă practic în urma procesului de extrapolare. Dar, după cum ne arată și legenda hărții, valorile erorilor se încadrează în limite rezonabile deci putem parcurge ultima etapă prin adăugarea tendinței câmpului interpolat TM0.
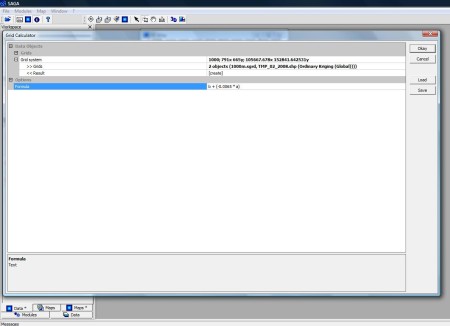
Ultimul pas parcurs în realizarea harții de necesită utilizarea modelului numeric al terenului si a suprafeței interpolate TM0. Pentru adăugarea tendinței gridului TMO (TMP_02_2008.shp (Ordinary Kriging (Global))) vom folosi funcția Grid Calculator din modulul Grid-Calculus, unde introducem formula b + (-0.0065 * a). La fel ca și în Table calculator, unde coloanele tabelului sunt indexate prin litere, și în Grid Calculator gridurile sunt de asemenea indexate prin litere, MNT-ului atribuindu-se litera a iar gridului TM0 litera b (figura 7).
Figura 7. Introducerea formulei în Grid Calculator.
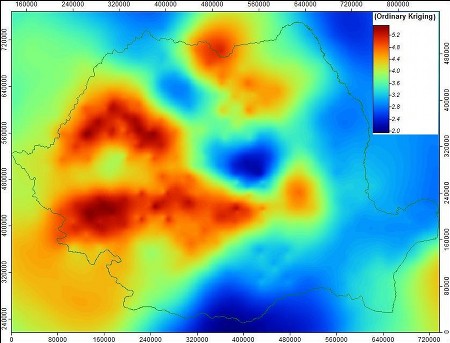
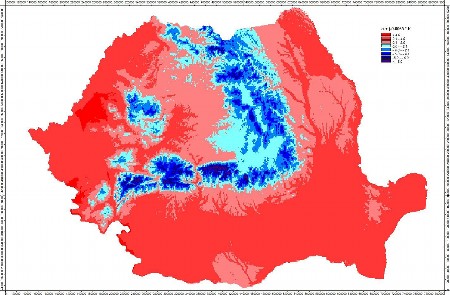
În urma calculului realizat obținem gridul care reprezintă distribuția spațială a temperaturii aerului pentru luna februarie 2008 (figura 8). Se poate observa strânsa dependență dintre valorile de temperatură și altitudine, cele mai scăzute valori de temperatură regăsindu-se în zonele înalte din Carpații Meridionali (sub -8.0 ° C) iar cele mai ridicate în partea de vest a țării si o mică parte din Culoarul Dunării (peste 4.0 ° C).
Figura 7. Temperatura medie lunară – februarie 2008.
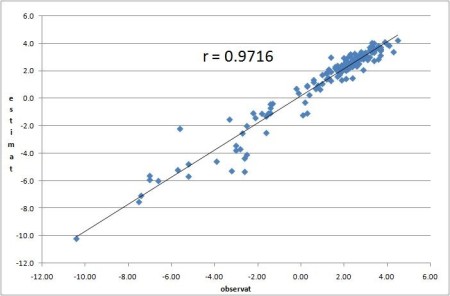
Pentru a verifica gradul de eroare al metodei de spațializare se face o analiză statistică între valorile observate si cele estimate. Prin aplicarea celui mai simplu criteriu de validare, coeficientul de corelație r (coeficientul Pearson), remarcăm valoarea acestuia apropiată de 1, valoarea 1 semnificând o perfectă pozitivă corelație între valorile măsurate și cele estimate. Pentru a extrage valorile estimate din gridul temperaturii medii lunare am folosit funcția Grid Values to Points din modulul Shapes-Grid.
Figura 9. Temperatura observată vs. estimată.
Prin cele prezentate sper că am reușit să exemplific funcționalitatea uneia dintre cele mai user -friendly aplicație open GIS, aplicație care suportă și posibilitatea automatizării funcțiilor utilizând scripturi DOS batch (saga_cmd.exe) sau mai nou prin folosirea interfeței Python a SAGA-API.